Mathematics.com: The special linear group is normal in the general linear group

Saturday, September 5, 2015

The special linear group is normal in the general linear group

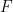Let $F$ be a field and $n$ a positive integer. Prove that $SL_n(F)$ is normal in $GL_n(F)$ and describe the isomorphism type of $GL_n(F)/SL_n(F)$ .

Let $A \in SL_n(F)$ and $B \in GL_n(F)$ . Now $\mathsf{det}(BAB^{-1}) = \mathsf{det}(B) \mathsf{det}(A) \mathsf{det}(B)^{-1} = \mathsf{det}(A) = 1$ , since multiplication in $F$ is commutative. Thus $BAB^{-1} \in SL_n(F)$ . Hence $SL_n(F)$ is normal in $GL_n(F)$ .
Define a mapping by .
1. (Well-defined) Suppose $A,B \in GL_n(F)$ such that $AB^{-1} \in SL_n(F)$ . Then $\mathsf{det}(AB^{-1}) = 1$ , so that $\varphi(A) = \mathsf{det}(A) = \mathsf{det}(B) = \varphi(B)$ . Thus $\varphi$ is well defined.
2. (Homomorphism) We have $\varphi(\overline{A} \overline{B}) = \varphi(\overline{AB}) = \mathsf{det}(AB)$ $= \mathsf{det}(A) \mathsf{det}(B) = \varphi(\overline{A}) \varphi(\overline{B})$ . Thus $\varphi$ is a homomorphism.
3. (Injective) Suppose $\varphi(\overline{A}) = \varphi(\overline{B})$ . Then $\mathsf{det}(A) = \mathsf{det}(B)$ , and we have $\mathsf{det}(AB^{-1}) = 1$ , so that $AB^{-1} \in SL_n(F)$ . Hence $\overline{A} = \overline{B}$ , and $\varphi$ is injective.
4. (Surjective) For all $q \in F^\times$ , note that the matrix with $q$ in the $(1,1)$ entry, 1 in all other diagonal entries, and 0 in all off diagonal entries has determinant $q$ . Thus $\varphi$ is surjective.
Thus is a group isomorphism, so that

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)