INDICES
Large or small numbers are better expressed in terms of indices. A given number is written as a base raised to the index, that is (base)index. Bases and indices can be any real number. In the last chapter we have seen what are squares and cubes of numbers; for squares the index is 2, for cubes the index is 3. For square roots the index is (1/2) and for cube roots the index is (1/3). The base has to be a suitable number that together with the indices gives the correct number. If the index is n, then the resultant number is obtained by multiplying the base n times.
Laws of indices
We will state a few facts about indices and try to see their validity using all sorts of numbers. The laws are valid for all real numbers, but for the present syllabus, it is sufficient to consider only rational numbers.
1. am * an = a (m+n).
2. a (-m) = 1 / am.
3. am / an = a (m-n) , a  0.
0.
4. (am) n = a (m * n).
5. (a * b) m = am * bm.
6. (a / b) m = am / bm , b  0.
0.
7. a0 = 1.
Example 1 : Let us consider the base a = 2, let the value of indices m and n be m=4, n=5.
LHS : am * an = 24 * 25 = (2 * 2 * 2 * 2) * (2 * 2 * 2 * 2 * 2) = 16 * 32 = 512.
RHS : a (m+n) = 29 = 512.
Since LHS = RHS, hence it is proved that am * an = a (m+n).
Example 2 : Let us consider the base a = 10, let the value of indices m and n be m=2, n=3.
LHS : am * an = 102 * 103 = (10 * 10) * (10 * 10 * 10) = 100 * 1000 = 100000.
RHS : a (m+n) = 105 = 100000.
Since LHS = RHS, hence it is proved that am * an = a (m+n).
2. To prove that a (-m) = 1 / am.
Multiply both the LHS and the RHS by am
a (-m) * am = (1 / am) * am.
From first law of indices proved above, LHS becomes a (m-m) = a0.
In the RHS, the numerator and the denominator cancel each other out to give a resultant of 1.
Thus a (m-m) = 1, which means that a (-m) * am = 1.
This gives a (-m) = 1/ am.
3. From the above two proofs, the third law of indices
am / an = a (m-n) , a  0.
0.
can be easily deduced.
The condition a  0 is important, because if a = 0, the expression will become infinite.
0 is important, because if a = 0, the expression will become infinite.
If m > n, the index of the expression on the RHS, that is (m-n), will be a positive number.
If m < n, the index of the expression on the RHS, the is (m-n), will be a negative number. In this case the second law of indices will have to be applied to obtain the value.
4. To prove that (am) n = a (m * n)
Example 1 : Let us consider the base a = 7, let the value of indices m and n be m=2, n=5.
LHS : (am) n = (72) 5 = ( 7 * 7 ) 5 = 495 = 49 * 49 * 49 * 49 * 49 = 282475249 .
RHS : a (m * n) = 710 = 7 * 7 * 7 * 7 * 7 * 7 * 7 * 7 * 7 * 7 = 282475249 .
Thus, LHS = RHS, hence it is proved that (am) n = a (m * n) .
Example 2 : Let us consider the base a = 1/2, let the value of indices m and n be m=1, n=2.
LHS : (am) n = ( (1/2)1 )2 = (1/2)2 = ‡ * ‡ = º .
RHS : a (m * n) = (1/2)2 = ‡ * ‡ = º .
Thus LHS = RHS, hence it is proved that (am) n = a (m * n).
5. To prove that (a * b) m = am * bm.
Example 1 : Let us consider the base a = 2 and b = 3, let the value of index m be m = 2 .
LHS : (a * b) m = ( 2 * 3 )2 = 62 = 6 * 6 = 36 .
RHS : am * bm = 22 * 32 = 4 * 9 = 36 .
Thus LHS = RHS, hence it is proved that (a * b) m = am * bm.
Example 2 : Let us consider the base a = 4 and b = 9, let the value of index m be m = ‡ .
LHS : (a * b) m = ( 4 * 9 )1/2 = 361/2 = 6 .
RHS : am * bm = 41/2 * 91/2 = 2 * 3 = 6.
Thus LHS = RHS, hence it is proved that (a * b) m = am * bm.
6. From the 1st , 2nd and the 5th laws of indices the 6th law of indices can also be proved. Thus,
(a/b)m = am / bm , b  0.
0.
The condition b  0 is necessary, otherwise the expression will become infinite with 0 in the denominator.
0 is necessary, otherwise the expression will become infinite with 0 in the denominator.
7. The 7th law of indices a0 = 1 is already proved above in the 2nd law of indices.
Summary
The indices are a very easy and convenient method for expressing very large or very small numbers. In case of small numbers, the index is negative and in case of large numbers the index is positive. All the laws of indices are useful in many calculations. These laws are valid for all real numbers, whether integers or fractions.
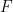 be a field and
be a field and  a positive integer. Prove that
a positive integer. Prove that  is normal in
is normal in  and describe the isomorphism type of
and describe the isomorphism type of  .
.and
. Now
, since multiplication in
is commutative. Thus
. Hence
is normal in
.
by
.
such that
. Then
, so that
. Thus
is well defined.
. Thus
is a homomorphism.
. Then
, and we have
, so that
. Hence
, and
is injective.
, note that the matrix with
in the
entry, 1 in all other diagonal entries, and 0 in all off diagonal entries has determinant
. Thus
is surjective.
is a group isomorphism, so that





